(Note 1: if you just want the LUTs and color space data, jump down to the section titled "The Data".)
(Note 2: this is a slightly odd post for this blog. I normally only write about things directly relevant to 3D rendering here, and this post has very little to do with 3D rendering. Although it is relevant to incorporating rendered VFX into footage if you're a Blackmagic user.)
When you're doing VFX work it's important to first get your footage into a linear color representation, with RGB values proportional to the physical light energy that hit the camera sensor.
Color in image and video files, however, is not typically stored that way1, but rather is stored in a non-linear encoding that allocates disproportionately more values to darker colors. This is a good thing for efficient storage and transmission of color, because it gives more precision to darker values where the human eye is more sensitive to luminance differences. But it's not good for color processing (such as in VFX), where we typically want those values to be proportional to physical light energy.
The functions that transform between non-linear color encodings and linear color are commonly referred to as transfer functions.2 There are several standard transfer functions for color, with sRGB gamma perhaps being the most widely known. But many camera manufacturers develop custom transfer functions for their cameras.3
If you're doing VFX work, you really want to know what transfer function your camera used when recording its colors. Otherwise you can only guess at how to decode the colors back to linear color.
Because of how important this is for a variety of use cases, pretty much every camera manufacturer documents and publishes their transfer functions. With two exceptions:
- Manufacturers of consumer-level cameras such as phones, pocket cameras, etc. (Totally reasonable, because these cameras are not intended for professional or semi-professional use.)
- Blackmagic Design.
Even the notoriously proprietary RED fully documents and publishes their transfer function in a freely available white paper. And that's because there's nothing proprietary or secret about transfer functions. They're about as proprietary as knowing which channels of your image data are red, green, and blue. You just need to know it to interpret your image data correctly.
So it's really odd and also very frustrating that Blackmagic hasn't done this basic due diligence. Blackmagic doesn't even provide this information to people who have purchased their cameras.4
(Update: after posting this, a couple of people pointed out that Blackmagic does have a white paper that documents the RGBW chromaticities15 and one of the transfer functions of their Gen 5 color spaces. However, there are two more Gen 5 transfer functions they don't document, and they haven't documented any of their other numerous color spaces. Moreover, it's nearly impossible to find this white paper unless you already know it exists and where it is, because it's buried in the installation of one of their smaller software tools. So my overall criticism still stands.)
Gotta Do It Yourself
Since Blackmagic hasn't published this basic information themselves, and since my work recently shot footage on a Blackmagic camera for a show with heavy VFX work, I took it upon myself to do Blackmagic's homework for them and reverse engineer their cameras' color spaces for publication here.
I want to emphasize again that all of this data is basic information that any professional or semi-professional camera manufacturer absolutely should publish about their cameras. This is no more proprietary than information about how to navigate a camera's menu system. It's just "how to use the camera", but for VFX people.
Methodology
There are a few places that already sell 3rd-party LUTs for Blackmagic cameras. Unfortunately, they're all oriented towards achieving "looks" with the footage, which is useless for VFX work. The color transformations we need for VFX are technical, not artistic.
Moreover, the places that sell these LUTs don't document how they make them, so even if they did publish linearization LUTs it would be hard to know if they were correct.
For that reason, I'm documenting here exactly how I created these LUTs. I'm also publishing the software tool I built for this purpose under an open source license so that others can reproduce and verify my work.5
Step 1
Although Blackmagic Design doesn't publish any information about their color spaces, they do provide a software tool called Resolve that, among other things, can linearize footage from their cameras.6 In other words, Resolve has all of Blackmagic's transfer functions built into it, just not in a way that is accessible as data or formulas.
But the great thing about color processing is that you can always compare results before and after. And that's the key idea behind determining Blackmagic's transfer functions.
I wrote a tool called LUT Extractor that generates a very specific OpenEXR image with gray, red, green, and blue gradients from 0.0 to 1.0, each with 2^17 steps. The image looks like this7:
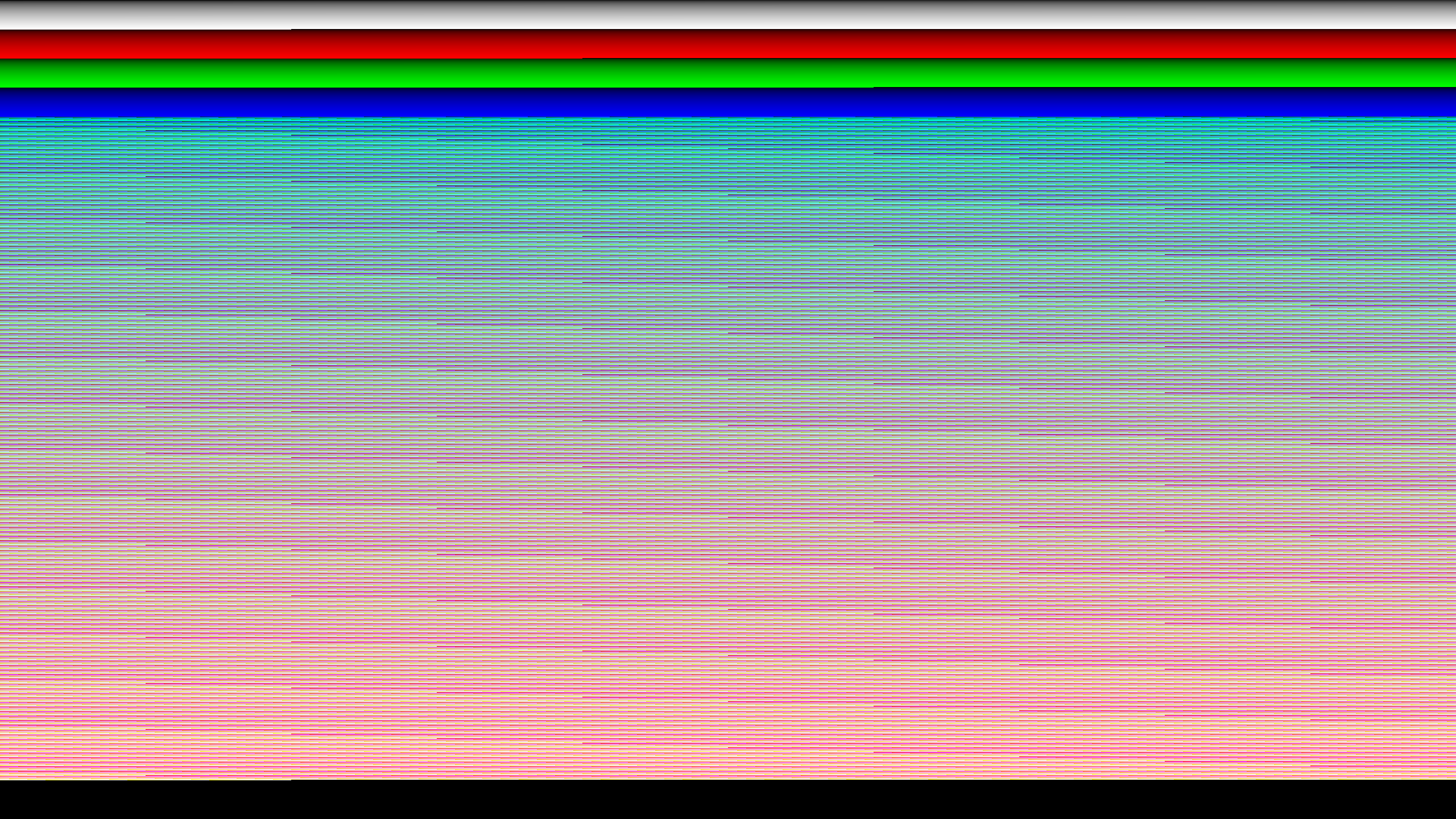
I then sent this image to a friend to pipe through Resolve (I wasn't able to install Resolve on my OS), once for each of Blackmagic's transfer functions.8 We transformed from encoded non-linear color to linear color for the exports, both because that's the transform we ultimately want to know and because the input for that is on a known, bounded interval. Linear color often exceeds the [0.0, 1.0] interval, whereas encoded color doesn't.
(Note: it's important to export at exactly the same resolution as the original image, and to do so as a lossless 32-bit floating point OpenEXR image.)
Step 2
I then piped those processed images back into LUT Extractor, which generates LUTs by mapping the colors from the original image to the processed image.
You can generate LUTs with 2^17 entries with this approach. But since that's overkill, I reduced them to 4096 entries, which is enough for 12-bit color without LUT interpolation.9
I used essentially the same process to determine the RGBW chromaticities of Blackmagic's color gamuts (which they also don't publish) as well. The only difference being that we stayed entirely in linear color and exported to CIE XYZ color space for that.
Step 3
Having LUTs for the transfer functions is already more than enough for most purposes. But there are situations where analytic formulas are better. For example, implementing the transfer functions in software.
To accommodate those use cases I also reverse engineered analytic formulas for a subset of the transfer functions. Specifically, the log footage subset.
Most log transfer functions use essentially the same formula, just with different constants. There are some minor variations of the formula, but they're all basically the same.10 Blackmagic's log transfer functions are no exception.
With the basic formula in hand, we just need to find the constants that match the target LUT. And it turns out this is pretty straightforward with a bit of iterative optimization.
My first attempt at this was to just throw some common optimization algorithms at the problem. And that worked fine—I got fits that were more than good enough for any practical purpose. But it turns out we can do even better thanks to the nature of the formula.
The standard log footage formula is a piecewise function consisting of a small linear segment near zero and a shifted/scaled logarithm for the rest of it. Both the linear and log parts have only a single free parameter if we keep the end points fixed, and we already know the end points from the first and last entries of the LUT. Moreover, the error metric for both the linear and log part have no local minimums other than the global minimum.
This means we can use a really simple iterative optimization algorithm that converges very quickly and very precisely (similar to but slightly more complex than a binary search) on each of the two parts separately.
With the exception of the Pocket Film transfer functions11, the resulting formulas match the LUTs with an average relative error of about 1/10,000th of a percent, and a maximum relative error of less than 1/100th of a percent.
In other words, for all practical purposes, the formulas are exact.
Blackmagic also has several non-log transfer functions. I haven't attempted to determine their formulas12, but the LUTs are still available.
The Data
So with that out of the way, here are Blackmagic Design's color spaces. For convenience, all names match what they are in Resolve's UI (at the time of posting), minus the "Blackmagic Design" prefix.
Transfer Function LUTs
Download (641 KB): Blackmagic Design - Transfer Function LUTs - 2022-04-23.zip
These are the linearizing LUTs (encoded color -> linear color). If you need the reverse LUTs (linear color -> encoded color) feel free to email me and I'll generate and post those too.
Both .cube and .spi1d formats are included.
Transfer Function Formulas (log only)
These are listed in pseudo code, along with the maximum and average relative error13 compared to the original values in the corresponding LUT.
ln is the natural logarithm, ^ is exponentiation, and e is the standard mathematical constant e.
All constants were computed in 64-bit precision, and are listed with that full precision.14
4K Film:
- Max Relative Error: 0.0000145
- Avg Relative Error: 0.0000007
A = 3.4845696382315063
B = 0.035388150275256276
C = 0.0797443784368146
D = 0.2952978430809614
E = 0.781640290185019
linear_to_log(x) =
if x <= 0.005000044472991669:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.0528111534356503:
(x - B) / A
else:
e^((x - E) / D) - C
4.6K Film Gen3:
- Max Relative Error: 0.0000336
- Avg Relative Error: 0.0000007
A = 4.6708570973650385
B = 0.07305940817239664
C = 0.0287284246696045
D = 0.15754052970309015
E = 0.6303838233991069
linear_to_log(x) =
if x <= 0.00499997387034723:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.09641357161134774:
(x - B) / A
else:
e^((x - E) / D) - C
Broadcast Film Gen 4:
- Max Relative Error: 0.0000166
- Avg Relative Error: 0.0000014
A = 5.2212906000378565
B = -0.00007134598996420424
C = 0.03630411093543444
D = 0.21566456116952773
E = 0.7133134738229736
linear_to_log(x) =
if x <= 0.00500072683168086:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.026038902009648163:
(x - B) / A
else:
e^((x - E) / D) - C
Film:
- Max Relative Error: 0.0000146
- Avg Relative Error: 0.0000007
A = 4.969340550061595
B = 0.03538815027497705
C = 0.03251848397268609
D = 0.1864420102390252
E = 0.6723093484094137
linear_to_log(x) =
if x <= 0.004999977151237935:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.060234739482005174:
(x - B) / A
else:
e^((x - E) / D) - C
Film Gen 5:
- Max Relative Error: 0.0000098
- Avg Relative Error: 0.0000007
A = 8.283611088773256
B = 0.09246580021201303
C = 0.0054940711907293955
D = 0.08692875224330131
E = 0.5300133837514731
linear_to_log(x) =
if x <= 0.004999993693740552:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.13388380341727862:
(x - B) / A
else:
e^((x - E) / D) - C
Pocket 4K Film Gen 4:
- Max Relative Error11: 0.0065348
- Avg Relative Error: 0.0002885
A = 4.323288448370592
B = 0.07305940818036996
C = 0.03444835397444396
D = 0.1703663112023471
E = 0.6454296550413368
linear_to_log(x) =
if x <= 0.004958295208669562:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.09449554857962233:
(x - B) / A
else:
e^((x - E) / D) - C
Pocket 6K Film Gen 4:
- Max Relative Error11: 0.0059241
- Avg Relative Error: 0.0002745
A = 4.724515510884684
B = 0.07305940816299691
C = 0.027941380463157067
D = 0.15545874964938466
E = 0.6272665887366995
linear_to_log(x) =
if x <= 0.004963316175308281:
x * A + B
else:
ln(x + C) * D + E
log_to_linear(x) =
if x <= 0.09650867241866573:
(x - B) / A
else:
e^((x - E) / D) - C
Gamut Chromaticities
These are given in CIE 1931 chromaticity coordinates.
(Note: the 4.6K Film Gen 1 chromaticities are missing because it doesn't seem to be a simple chromaticity transform. It's possible we screwed up the export from Resolve. If you need it, feel free to get in touch and we can try again.)
Wide Gamut Gen 4/5:
| x | y | |
| R | 0.717722 | 0.317118 |
| G | 0.228041 | 0.861569 |
| B | 0.100584 | -0.082045 |
| W | 0.312700 | 0.329000 |
4K Film Gen 1:
| x | y | |
| R | 0.742225 | 0.285898 |
| G | 0.414011 | 1.303536 |
| B | 0.034208 | -0.083318 |
| W | 0.313544 | 0.330476 |
4K Film Gen 3:
| x | y | |
| R | 1.062492 | 0.394762 |
| G | 0.368934 | 0.777492 |
| B | 0.095603 | 0.033224 |
| W | 0.313544 | 0.330476 |
4.6K Film Gen 3:
| x | y | |
| R | 0.860829 | 0.368869 |
| G | 0.328213 | 0.615591 |
| B | 0.078252 | -0.023256 |
| W | 0.312700 | 0.329000 |
Film Gen 1:
| x | y | |
| R | 0.917258 | 0.250238 |
| G | 0.283328 | 1.707231 |
| B | 0.085572 | -0.070780 |
| W | 0.313538 | 0.330465 |
Pocket 4K Film Gen 4:
| x | y | |
| R | 0.717722 | 0.317118 |
| G | 0.228041 | 0.861569 |
| B | 0.100584 | -0.082045 |
| W | 0.312700 | 0.329000 |
Video Gen 4:
| x | y | |
| R | 0.682777 | 0.318592 |
| G | 0.237613 | 0.813547 |
| B | 0.121743 | -0.044283 |
| W | 0.312700 | 0.329000 |
Video Gen 5:
| x | y | |
| R | 0.640000 | 0.330000 |
| G | 0.300000 | 0.600000 |
| B | 0.150000 | 0.060000 |
| W | 0.312700 | 0.329000 |
Footnotes
-
There are exceptions, of course. OpenEXR stores color linearly (at least, if you ignore the nature of floating point numbers). And many raw formats are also linear.
-
"Transfer function" is actually a more general engineering term, but in the context of color this is always what it means.
-
And this is for good reason: most standardized transfer functions are designed to encode colors for final delivery and display, which has different considerations than encoding colors that may undergo further processing (e.g. in VFX and color grading).
-
I don't mean to be too critical of Blackmagic here. They make excellent cameras at a shockingly cheap price point for what they're capable of. I don't have anything against Blackmagic except for their extreme laziness on this point. (Well, that and them claiming to have created an "open standard" raw format that they've also failed to document and which is only accessible via a closed-source SDK. It might be a good raw format, but I don't think they know what "open standard" means.)
-
Which is also valuable because I'm human and make mistakes! Also, this way if Blackmagic comes out with additional color spaces in the future, people aren't dependant on me for figuring them out.
-
This is great if you can go through Resolve, but there are situations where you may want or need to do your color processing via other tools. It's also important information when archiving footage, where (when possible) you want to include metadata about how to properly interpret the color data, such as chromaticity primaries and the transfer function used for encoding.
-
This has been converted to PNG for online viewing purposes, but the original is a full 32-bit floating point OpenEXR image and can be easily generated with the linked tool. Also, the funky stuff below the gradients is a 144x144x144 3D RGB cube. I'm not using that part yet, but it will be useful if I ever need to get 3D LUTs in the future.
-
This turned out to be unexpectedly tricky because Resolve really wants to do additional color processing beyond just color space conversion. Our first attempts resulted in LUTs that had filmic s-curves baked in, etc., which I guess are just defaults in Resolve. That might make sense for color grading, but thwarts actually linearizing footage for VFX purposes. We did eventually figure out how to get Resolve to do what we needed, though.
-
With LUT interpolation it's likely more than enough for any bit depth. You actually don't need much resolution in non-linear -> linear LUTs to achieve very high precision because of how they typically curve. You do need a lot of resolution for LUTs going the other way, however. This is in fact another reason we exported from Resolve in the non-linear -> linear direction.
-
This makes sense because there's basically no reason to innovate here, if "innovate" is even a sensical term in this context.
Having said that, there is room for innovation when designing transfer functions for delivery rather than capture. For example, the Perceptual Quantizer is a transfer function designed to closely approximate the human visual system's response to luminance, which is really useful for storing and broadcasting finished media using minimal data.
But for transfer functions intended for capture, the existing standard formulas are more-or-less optimal, and just need the constants tweaked for the capture hardware's noise floor and dynamic range.
-
The less precise fit of these two transfer functions is because Blackmagic didn't quite implement them correctly: the linear and log parts of the curve aren't aligned precisely, so there's a small discontinuity where they're supposed to meet. You can see this yourself if you graph the LUTs: zoom in around x=0.095 and you can see a little blip in both transfer functions.
-
Although, interestingly, Blackmagic Design Video (sans any "Gen #" postfix) turns out to be identical to the Rec.709 transfer function. I only noticed this while checking graphs of the generated LUTs.
-
I list relative error rather than absolute error because relative is a better metric for color transfer functions—small changes in dark values are far more important than small changes in bright values. Relative error is computed as:
abs(fitted - original) / abs(original) -
This is certainly way overkill given the relative error of the fits. But I figured listing them in the full computed precision doesn't hurt.
-
It's also interesting to note that the white point they document in their paper for Gen 5 doesn't quite match the white point they use in Resolve for Gen 5 (the latter is in my listings). It's not different enough to make a practical difference, though—both are D65, just with different precision. And it would be an easy software update, so this footnote may become outdated pretty quickly.
