In Building a Better LK Hash I developed a significantly improved variant of the Laine-Karras hash for base-2 Owen scrambling. And in Owen Scrambling Based Blue-Noise Dithered Sampling I used base-4 Owen scrambling to build a simpler implementation of Ahmed and Wonka's screen-space blue-noise sampler. But there's an annoying gap between those two posts: unlike base-2, there's no fast hash for performing base-4 Owen scrambling, so you have to resort to a slower implementation.

In this post I'm going to fill that gap by developing a Laine-Karras style hash for base-4 Owen scrambling as well.¹

Here's the hash we're going to end up with:

n ^= x * 0x3d20adea
n ^= (n >> 1) & (n << 1) & 0x55555555
n += seed
n *= (seed >> 16) | 1
n ^= (n >> 1) & (n << 1) & 0x55555555
n ^= n * 0x05526c56
n ^= n * 0x53a22864

You might notice that this is identical to the base-2 hash from my LK hash post, except for the addition of this line in two places:

n ^= (n >> 1) & (n << 1) & 0x55555555

And it's this line that I'll be explaining in this post.

If you haven't already, you should probably read my LK hash post, because this post builds on the concepts I introduce in that.

(Note: the above hash is semi-ad-hoc, in the sense that I haven't optimized it for quality like I did the base-2 hash. However, the construction used to build it—which I cover in this post—is not ad-hoc, and can likely be the basis of a higher quality hash in the future.² In other words, the hash in this post is akin to the original Laine-Karras hash: it's good enough for many practical applications, but isn't especially high quality.)

Base-2 is almost base-4.

The key idea behind this new hash is that base-4 Owen scrambling is a strict superset of base-2. In other words, base-4 Owen scrambling contains all the permutations of base-2, and then some additional ones as well. So the goal is to find a way to introduce those missing permutations into the base-2 hash.

To revisit base-2 Owen scrambling briefly, it does a random hierarchical shuffle of equal segments of two. For example, a two-level scramble looks like this:

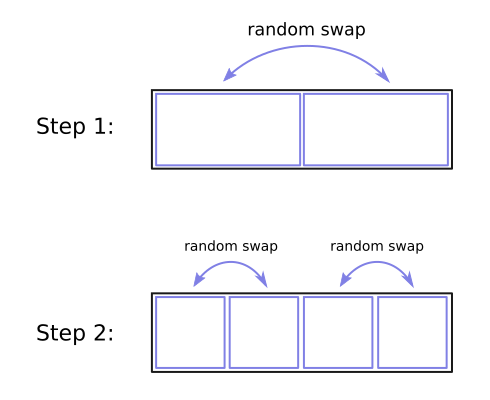
By contrast, base-4 Owen scrambling does a hierarchical shuffle of four segments. Which means at each level it's doing a full shuffle of four segments at once, like this:

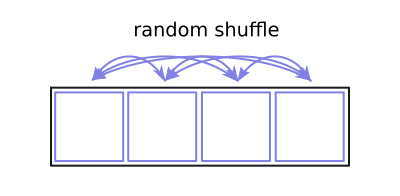
So if we have four segments, A, B, C, and D:

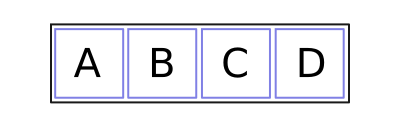
...base-4 scrambling can put them in any order, but base-2 is more limited. To illustrate this a little better (and in a way that's useful for the rest of this post) we can also visualize this with quadrants:

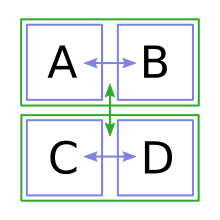
Base-2 scrambling can swap A with B, C with D, and the top half with the lower half. But it can't individually swap A with C, for example. Base-4 scrambling, on the other hand, can shuffle the quadrants however it likes.

Base-4 as a base-2 sequence.

It turns out, however, that we can build a base-4 shuffle out of a sequence of base-2 shuffles on different axes. Specifically, if we have a sequence of random swaps like this:

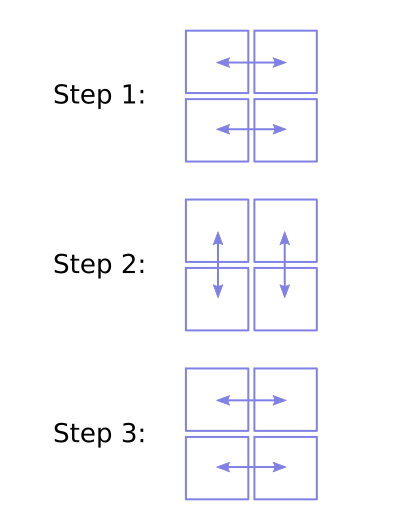
...then we have a full base-4 shuffle—the quadrants can end up in any configuration.

Given a base-2 hash, one way to accomplish that three-step process is this:

n = base2_hash(n)
n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1)
n = base2_hash(n)
n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1)
n = base2_hash(n)

The lines between the hashes are just taking each pair of bits and swapping their left/right bits, like this:

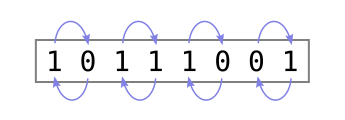
Each pair of bits represents a level of quadrants, with the right bit representing the vertical (y) position and the left bit the horizontal (x) position:

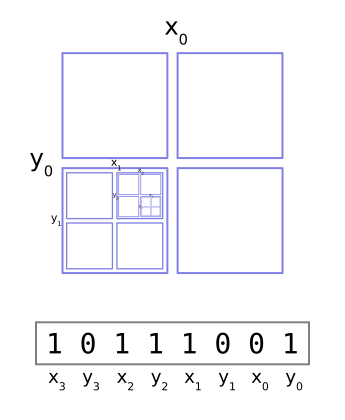
When the x bit is 0 we're on the left and when it's 1 we're on the right. Correspondingly, y=0 is the top and y=1 is the bottom. In other words, they're just coordinates into our nested quadrant hierarchy.

So the reason the above hash -> bit-swap -> hash -> bit-swap -> hash construction works is because we're effectively swapping the x/y axes of our quadrants between shuffles, so that the middle shuffle can do independent swaps on the vertical axis. Which is exactly what we need for our three-step shuffle.

It's worth noting, however, that this three-step approach isn't statistically even. In other words, although a three-step shuffle can produce all possible configurations, it doesn't produce them with equal probability even if each step is perfectly random. Uniform statistics is important for a base-4 Owen hash of high quality, so this isn't ideal. But let's set that aside for the time being—I'll come back to it later.

Doing it faster.

So that already works fine, and performs a base-4 Owen scramble on reversed bits. But it's also roughly 3 times as slow as the base-2 hash because... well, it's executing the base-2 hash three times! So how can we do better?

From a hashing perspective, a lot of randomness has already been injected into our integer after the first round of hashing. So one way we can improve things is by doing our vertical swaps based on that already-present randomness.

To do that, we'll need a way to directly perform our independent vertical swaps, rather than going through our indirect swap-hash pattern.

Fortunately, this is relatively straightforward. Since the left bit of every pair represents our horizontal position, we can shift that over and xor it with the right bit (our vertical position) to do a vertical swap that's conditional on which side it's on:

n ^= (n >> 1) & 0x55555555

(Note: for those not well-versed in hex, 0x55555555 is just ...01010101 in binary.)

This construction will unconditionally swap the right side, and not the left side. It's actually okay to never swap the left side because the base-2 scramble already (randomly) does a top-half/bottom-half swap. A combination of that and a random right-side vertical swap can produce any combination of left/right vertical swaps.

But we do still need the right-side swap to be random, not unconditional as above.

To make it random, we use the randomness from the bits lower than the pair. We shift the highest lower bit³ up and do a bit-wise & with it to conditionally mask the effect of the higher bit:

n ^= (n >> 1) & (n << 1) & 0x55555555

And that's where the line from the start of the post comes from: it's a random right-side vertical swap. With this new tool in our toolbox, we can now simplify our base-4 hash to this:

n = base2_hash(n)
n ^= (n >> 1) & (n << 1) & 0x55555555
n = base2_hash(n)

Doing it even faster.

But we can potentially make this even faster. Let's revisit the base-2 hash again:

n ^= n * 0x3d20adea
n += seed
n *= (seed >> 16) | 1
n ^= n * 0x05526c56
n ^= n * 0x53a22864

Every line of this hash is doing base-2 scramble-like things. You can take pretty much any part of this hash on its own, and it's kind of a poor-quality base-2 hash.

So the question is: are there places in the middle that we can insert our new line and be "good enough"? Where the parts of the base-2 hash that come before and after do enough base-2 mixing to get that horizontal-vertical-horizontal scrambling effect?

To answer this question I literally just tried inserting the new line in a bunch of different places, and eyeballed how the results looked when applied to the screen-space blue-noise technique in my previous post. I also wrote some bespoke code to check the statistics of the quadrant permutations.⁴

And that's how I ended up with the hash at the start of this post. Here's that hash again:

n ^= x * 0x3d20adea
n ^= (n >> 1) & (n << 1) & 0x55555555
n += seed
n *= (seed >> 16) | 1
n ^= (n >> 1) & (n << 1) & 0x55555555
n ^= n * 0x05526c56
n ^= n * 0x53a22864

Surprisingly, the permutation statistics⁴ of this hash aren't completely awful. Once you get past the lowest 8 bits, all 24 permutations of the quadrants are produced pretty often. And even after just the lowest 6 bits, around 21-23 permutations are produced pretty often. Keeping in mind that it's impossible to hit all permutations until you get past the first 6 bits (4 bits = 16 possible states), that's not bad.

Having said that, the permutations are definitely not equally probable, with the most likely permutation being roughly twice as likely as the least likely one.⁵ That's about the statistics you would expect from the earlier three-step construction as well, so it's at least not worse than that. But in terms of being high quality, that still leaves a lot to be desired.

Nevertheless, this hash appears to be more than good enough for the screen-space blue-noise sampling technique. And I suspect is good enough for many other practical applications as well.

Wrapping up.

The hash in this post is not high quality, which leaves a lot of room for improvement. I strongly suspect that a much higher quality hash can be achieved with optimization techniques similar to those in Building a Better LK Hash. New quality metrics would need to be developed, of course, since the behavior of base-4 Owen scrambling is different. But in terms of randomly generating potential hashes, just adding n ^= (n >> 1) & (n << 1) & 0x55555555 to the pool of valid component operations should, I think, be enough.

But for the time being, this hash is still really useful. In particular, it seems to be great as a drop-in replacement for the slower base-4 Owen scramble in Owen Scrambling Based Blue-Noise Dithered Sampling.

Footnotes

1. A brief reminder: like the Laine-Karras hash, to perform Owen scrambling with this hash you need to run it on an integer with its bits in reverse order. So an Owen scramble would be reverse_bits(hash(reverse_bits(n))).

2. I suspect I'll take a crack at a high-quality base-4 hash at some point, unless someone beats me to it (which would be great!). And if I do, I will of course make a post about it.

3. It's important that we use the highest of the lower bits here, because that's the one that has itself been influenced by all the bits lower than it in the earlier hashing. Thus by using it, our random masking choice is affected by all the lower bits.

4. I'm hand-wavey about the specifics here, because the measures I used are themselves a bit hand-wavey at this point.

5. Although you can actually improve this significantly by tossing in even more of the new line. For example, this:

   n ^= (n >> 1) & (n << 1) & 0x55555555
   n ^= x * 0x3d20adea
   n ^= (n >> 1) & (n << 1) & 0x55555555
   n += seed
   n *= (seed >> 16) | 1
   n ^= (n >> 1) & (n << 1) & 0x55555555
   n ^= n * 0x05526c56
   n ^= (n >> 1) & (n << 1) & 0x55555555
   n ^= n * 0x53a22864
   

   Achieves a ratio of just 1.2 between the least and most likely permutations, which is far better than the three-step construction, and less expensive as well.

   I didn't put this variant in the main post because, practically speaking, I don't think there's a good argument for using it. It's very likely not great quality in other ways because (as stated in footnote 3) my measures are pretty hand-wavey at this point. And if we're trying to minimize metrics, we really want something more robust.